3. A termelési függvény jellemzői

A skálahozadéki függvény megmutatja, hogy ha a termelési tényezők mennyiségét azonos mértékben változtatjuk, hogyan változik a termelés.

A skálahozadéki függvény azt feltételezi, hogy a vállalat már kiválasztott egy technológiát, azt nem változtatja meg, de adott technológia mellett meg tudja változtatni mindkét termelési tényező mennyiségét, változatlanul hagyva a tényezőarányokat.

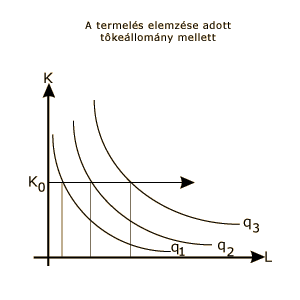
A termelési felületből metszeteket készítve kétdimenziós alakzathoz jutunk. A termelési függvényt kétdimenziós formában ábrázolhatjuk, ha a termelési tényezők terében vesszük fel azokat a pontokat, amelyek azonos termelési mennyiséget eredményeznek. A megoldás a következő:

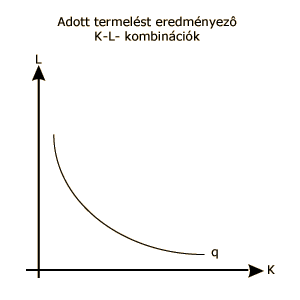
Legyen ez az adott termelési mennyiség q! Ezen termékmennyiséget a q magasságú egyenesek jelölik az ábrán. A vastag vonal azon tényezőkombinációkat jelöli ki, amelyekkel ezt a q mennyiséget elő lehet állítani. Ha a háromdimenziós termelési "dombot" q magasságban elmetsszük a K-L-koordinátákkal párhuzamos síkkal, akkor jutunk ehhez a vastag vonalhoz. Ha ezeket a kijelölt pontokat egy olyan koordináta-rendszerben ábrázoljuk, ahol a vízszintes tengelyen a munka, a függőleges tengelyen a tőke mennyiségét mérjük, akkor egy olyan görbét kapunk, amelyik a tőke és munka azon kombinációit tartalmazza, amelyek q termelési mennyiséget eredményeznek adott termelési függvény esetén. Ezeket a görbéket isoquantoknak, vagyis egyenlő-termék görbéknek nevezzük.

Ha például a termelési függvény alakja , akkor a kimetszett függvényünk egyenlete: , ahol q egy adott érték A függvény explicit formája: , ahol q konstans. A függvény grafikus alakját láthatjuk a 34. ábrán.

4. Az egymást korlátozottan helyettesítő tényezők és a termelés kapcsolata

A fentiekben minden tényező – kibocsátás kapcsolatot folyamatosnak ábrázoltunk: azt feltételeztük, hogy az egyes tényezők oszthatóak és helyettesítik egymást. Ha ez nem valósul meg maradéktalanul, akkor a termelési függvény nem egy folyamatos felület, hanem egy táblázat segítségével írható le. Egy ilyen táblázatból is kikereshetjük a megfelelő isoquant értékeket, de nem egy folyamatos görbét, hanem egy ponthalmazt kapunk.

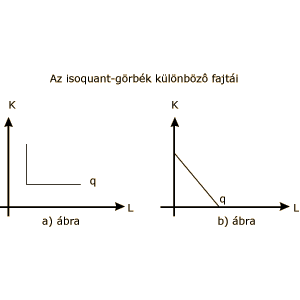
Ha a tényezők egyáltalán nem oszthatóak, akkor a helyettesítés még korlátozottan sem érvényesül, a tényezőarányok teljesen merevek. Egy-egy termékegységet csak meghatározott mennyiségű tőkével és munkával lehet előállítani.

Ebben az esetben a termék előállítása technikailag csak egyetlen hatékony tőke-munka aránnyal lehetséges, akkor változatlan termelés csak úgy képzelhető el, hogy az egyik tényező mennyiségét növelve a másik mennyiségét nem változtatjuk. Sőt, ez a megoldás tulajdonképpen értelmetlen, hiszen ezzel technikailag nem hatékony megoldáshoz jutunk. Elméletileg azonban felrajzolhatunk egy ilyen isoquantot, mint például a 36. a) ábrába.

36. ábra

A helyettesítés azonban még ebben az esetben sem teljesen lehetetlen, ha létezik több ilyen termelési eljárás. Ezt a helyzetet egy sajátos termelési függvény és isoquant rendszer írja le, amit első elemzője utána Leontief-féle termelési függvénynek nevezünk. A függvényt és belőle levezethető törtvonalú isoquantot itt ismerheti meg.

5. Ráfordítás és a kibocsátás kapcsolata tökéletesen osztható tényezők esetén

A folyamatos termelési függvény legfontosabb jellemzője a homogenitása. Egy termelési függvény akkor homogén, ha a függvény teljes értelmezési tartományában azonos jellegű a skálahozadék.

A homogén függvények jellemzője a homogenitás foka.

Egy termelési függvény r-ed fokú homogén, ha a tényezőket 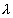-szorosára növelve a termelés 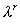-en szeresére növekszik, a függvény teljes értelmezési tartományán belül.

(32)