| Vissza |
Az egyenletes és egyensúlyi növekedés mellett az egy főre jutó tőkeállomány és az egy főre jutó kibocsátás állandó, mert Y, K és N azonos ütemben növekszik. Mekkora ez az optimális Y/N és K/N?
A válaszhoz meg kell vizsgálnunk a tőkeállomány növekedésének jellemzőit. A tőkeállomány növekménye nem más, mint a nettó beruházás: dK = I. Egyensúly esetén a beruházás megegyezik a megtakarítással (S = I). A megtakarítást meghatározhatjuk a kibocsátásból a megtakarítási hányad segítségével: S = sY. Növekedési modellünk feltevése és Simon Kuznets korábban idézett számításai szerint a megtakarítási hányad hosszú távon állandó, ezért a beruházás csak a kibocsátás nagyságától függ:
A tőkeállomány növekedési ütemét megkapjuk, ha 110. képlet mindkét oldalát elosztjuk K-val:
A 111. képlet jobb oldalán levő kifejezést átalakíthatjuk úgy, hogy abban az egy főre jutó termelés és az egy főre jutó tőkeállomány szerepeljen. Ennek érdekében a számlálót és a nevezőt el kell osztani N-nel:
Egyensúly esetén a tőkeállomány növekedési ütemének meg kell egyeznie a munkaképes népesség növekedési ütemével. Jelöljük az utóbbit gN-nel! ![]() Az egyensúlyi és egyenletes növekedés feltétele tehát:
Az egyensúlyi és egyenletes növekedés feltétele tehát:
Az egyenletben szereplő gN és s adott és változatlan értékek. Az egy főre jutó kibocsátás (y) pedig 109. képlet alapján csak k-tól függ. (Ne felejtsük el, hogy a technikai haladást figyelmen kívül hagytuk, és a tőke termelési rugalmassága konstans!) Eszerint a 113. képletben egyetlen változó van, ez a k, ami meghatározza y értékét. Az egyenletes és egyensúlyi növekedés azon egy főre jutó kibocsátás és egy főre jutó tőkeállomány mellett valósul meg, ami kielégíti az alábbi feltételt:
Az egyensúly meghatározását elvégezhetjük grafikusan is.
|
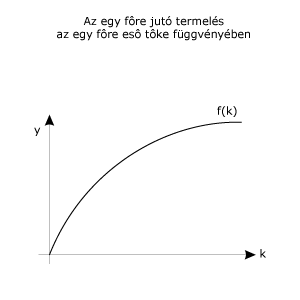
Az egy főre jutó kibocsátás az egy főre jutó tőkeállomány növekedésével lassuló ütemben nő - hasonlóan a rövid távú termelési függvényhez. | ||
|
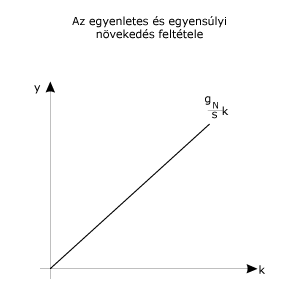
A 114. képletben szereplő egyensúlyi feltételt felfoghatjuk egy olyan egyenes egyenleteként, amelyik minden k-hoz hozzárendel egy y-t, mégpedig a |
||
|
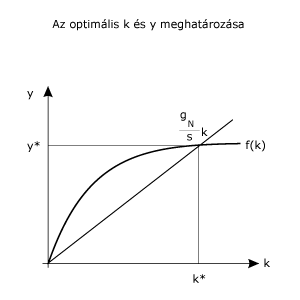
Ha a két függvényt egy koordináta-rendszerben ábrázoljuk, akkor láthatjuk, hogy csak egyetlen közös pontjuk lehet (a k*, y* kombináció). |
| Vissza |