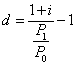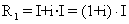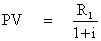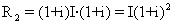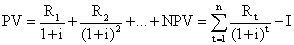Jelenérték-számítás

Mindenekelőtt néhány fogalom pontosítására van szükség.

A kamat nagysága a kölcsönadott pénzösszegtől és a kamatlábtól függ.

A kamatlábat rendszerint egy évre határozzák meg, így a fizetendő kamat összege függ a hitel időtartamától is.

A nominális kamatlábbal kiszámított kamat nagysága azonban nem egyezik meg minden esetben a kölcsönadó jövedelmével. Ha az árszínvonal növekszik a kölcsön időtartama alatt, akkor a kölcsönadott pénzösszeg reálértéke csökken. Ezért a kamat egy része ezt a reálérték-csökkenést kompenzálja.

A reálkamatlábat szintén a kölcsönadott pénz százalékában határozzuk meg. A számítás során azonban nem a nominális kamatösszeget hasonlítjuk össze a kölcsönadott összeggel, hanem a nominális kamat reálértékét.

Ha az év elején kölcsönadunk 100 forintot és az év végén 110 forintot fogunk visszakapni, akkor a nominális kamatlábat egyszerűen meghatározhatjuk, ha a kamatösszeget elosztjuk a kölcsönadott összeggel: 10/100 = 0,1, vagyis a nominális kamatláb 10 százalék. Ha azonban az év során az árszínvonal 5 százalékkal növekedett, akkor az év végén kapott 110 forint reálértéke már csak 104,75, így a reálkamatláb csak 4,75 százalék.

A reálkamatlábat kiszámíthatjuk a nominális kamatláb és az árindex ismeretében. A nominális kamatlábat i-vel, a reálkamatlábat d-vel jelölve a számítás módja a következő:

(55)

Közelítő eredményt kapunk, ha a nominális kamatláb értékéből levonjuk az árak növekedési százalékát.

A fenti példában ez a közelítő érték: 10-5=5 százalék.

A piaci kamatláb a különböző lejáratú és kockázatú befektetések kamatlábainak (hozadéki rátáinak) súlyozott átlaga.

Mivel ebben a fejezetben mindvégig rögzített árakkal dolgozunk, ezért most a reálkamatláb megegyezik a nominális kamatlábbal.

Térjünk most át a beruházások értékelésére!

Induljunk ki egy egyszerű esetből: egy vállalat egy 600 ezer forint értékű gépet akar megvásárolni, amit egy évig tud használni. A gép értékének és a befektetendő összeg kamatának egy év múlva meg kell térülnie. Ha a beruházás segítségével a vállalat 1 millió forint bevételre számít, amiből fedezik a termelés folyó költségeit (anyag- és bérköltség stb.), ami 375 ezer forint, akkor a beruházás hozama 625 ezer forint. Ez a bevételnek az a része, amely fedezheti a befektetés költségeit és annak jövedelmét. A befektetés megtérülésén felül 25 ezer forint jövedelemre tehetnek szert, ami a befektetés 25/600=0,042, azaz 4,2 százaléka. Ha a piaci kamatláb ennél alacsonyabb, akkor érdemes a beruházást megvalósítani. Ha azonban a piaci kamatláb akár csak 5%, akkor ezt a beruházást nem érdemes megvalósítani, hiszen a pénzügyi befektetéssel (kötvény vásárlásával vagy bankbetéttel) nagyobb nettó jövedelemre tehetnek szert.

Kicsit nehezebb a számítás, ha a beruházás több éven keresztül térül meg. Ekkor a befektetés értékeléséhez kétféle számítási módszert választhatunk: az egyik lehetőség, hogy kiszámítjuk a várható hozamok jelenértékét, vagy pedig a befektetés hozadéki rátáját, a belső kamatlábat.

A jelenérték kifejezi, mennyit ér ma egy jövőben várható pénzbevétel. A fogalomnak és kiszámítási módszerének, a diszkontálásnak jobb megértése érdekében gondoljuk végig a következőket! Ha egy I összegű beruházástól (befektetéstől) azt várjuk, hogy egy év múlva éppen annyi nettó bevételt eredményezzen, mint amekkora bevételre a piaci kamatláb (i) mellett számíthatunk egy ugyanekkora összegű pénzügyi befektetéstől, akkor egy év múlva a beruházás hozamának (R₁) meg kell egyeznie a beruházás kamattal növelt összegével:

(56)

A beruházás tényleges hozama azonban nem feltétlenül egyezik meg ezzel az összeggel. R₁ lehet kisebb vagy nagyobb, mint a beruházás értékének 56. képlet szerint felkamatolt összege. A tényleges hozam megítélése érdekében ki kell számítanunk annak mai értékét, vagyis azt a befektetési összeget, amely átlagos piaci kamatláb mellett éppen R₁–t eredményez. Ez az összeg a várható hozam jelenértéke. Ha 56. képletben I helyébe a jelenérték jelét írjuk be, akkor az egyenlet átrendezésével megkapjuk a jelenérték (PV = Present Value) kiszámításának képletét.

(57)

Ha az így kiszámított jelenérték meghaladja a beruházás bekerülési értékét, akkor érdemes megvalósítani a beruházást.

Ha a beruházás csak egy évig üzemel, akkor ez a számítási módszer nem ad több információt, mint az előbbi példában alkalmazott egyszerű számítás. Ha azonban a beruházás két évig üzemel, és csak a második évben számíthatunk bevételre, akkor más lesz a helyzet. Legyen a beruházás hozama (a folyó költségek levonása után megmaradt összeg) R₂ ! Mekkora ennek az összegnek a jelenértéke? A befektetett összeg (vagy annak egy része) most két évig kamatozik, és természetesen nem áll módunkban az első év végén kivenni pénzünket, ezért kamatos kamattal kell számolnunk, a kamattal megnövelt összeg még egy évig kamatozik. A befektetett összeg (I) két év múlva várható bevétele a piaci kamatláb alapján:

(58)

Ebből 57. képlethez hasonlóan kifejezhetjük a beruházás második évben várható hozamának jelenértékét:

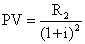
Ha a két évig üzemelő beruházásból az első évben R₁, a második évben pedig R₂ hozamra számítunk, akkor a beruházás jövedelmének teljes jelenértéke:

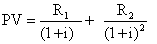
Kétéves használat esetén a beruházást akkor érdemes megvalósítani, ha ez a jelenérték nagyobb, mint a beruházás költsége (I). Most már pontosíthatjuk a jelenérték fogalmát!

Alkalmazzuk a megismert számítási módszert a fenti példára! Ha egy évig kapjuk csak a 625 ezer Ft jövedelmet , akkor egy 4 százalékos piaci kamatláb mellett kedvezőnek ígérkezik a 600 ezer forint befektetése. Számítsuk ki, hogy ha két éven keresztül kapjuk ugyanazt a bevételt, 4 százalékos piaci kamatláb mellett, akkor mennyi lehet az a maximális beruházási érték, amit érdemes befektetnünk a termelésbe? Ha nem végeznénk jelenérték-számítást, akkor azt mondhatnánk, hogy kétszer 600 ezer forintot érdemes befektetni, mert mindkét évben a piaci kamatnál nagyobb bevételre számíthatunk. A jelenérték-számítás azonban nem támasztja alá ezt a feltevésünket. A két év bevételének jelenértéke:

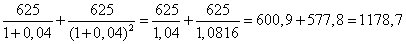
Ez az összeg kisebb, mint a beruházás fent feltételezett bekerülési értéke (1200 ezer), ezért 4 százalékos piaci kamatláb mellett ez a tőkeberuházás kevesebbet hozna, mint a pénzügyi befektetés.

Általánosítva az elmondottakat, a következő összefüggést kapjuk: ha egy beruházás n éven keresztül különböző jövedelmeket hoz, akkor az adott beruházásból várható összes hozam jelenértéke:

(59)

ahol R_t a beruházás t-edik évben várható hozama.

Az így kiszámított jelenérték a beruházás tőkésített értéke.

A beruházást akkor érdemes megvalósítani, ha a tőkésített érték meghaladja a beruházás bekerülési értékét, tehát PV > I.

Ha a beruházás tőkésített értékéből levonjuk a beruházás bekerülési értékét, akkor megkapjuk a beruházás nettó jelenértékét.

Kiszámításának képlete:

(60)