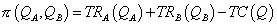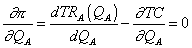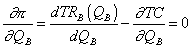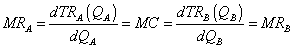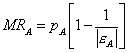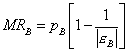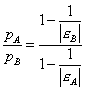A fogyasztói csoportokat gyakran nem csak az különbözteti meg egymástól, hogy alacsonyabb áron hajlandóak vagy tudnak-e többet vásárolni, hanem preferenciarendszerük alapján is jól elkülöníthetők egymástól. A sznobok csak márkás pólót, sampont vagy cipőt vásárolnak, mások viszont előnyben részesítik az olcsó „no name” termékeket, a fiatalok és a középkorúak nem egyforma összeget hajlandóak ugyanazon szórakozási lehetőségért fizetni stb. Ha az eladó jól elkülöníthető fogyasztói csoportoknak értékesíti termékét, akkor ugyanazt a terméket és ugyanazt a mennyiséget eltérő áron tudja eladni.

A fő kérdés az, milyen árat állapítson meg a termelő a két vagy több csoport számára? Eddigi ismereteink alapján viszonylag könnyen megérthetjük a megoldást. Tegyük fel, hogy a vizsgált monopólium két vevői csoportnak tudja termékét értékesíteni, akiknek keresleti függvénye lényegesen eltér egymástól, az egyik jóval rugalmasabb, mint a másik. Az optimális megoldás megtalálása érdekében két dolgot kell belátni – a határbevételek egymáshoz való arányát, valamint a határbevételek és a határköltség kapcsolatát.

Akármennyit is termel összesen a vállalat, úgy kell megosztani az eladási mennyiséget a két csoport között, hogy mindkét csoport esetében azonos legyen az értékesített mennyiséghez tartozó határbevétel. Ha ugyanis az egyik csoportban nagyobb lenne a határbevétel mint a másikban, akkor érdemes lenne ide átcsoportosítani az értékesítés egy részét, hiszen változatlan ráfordítás mellett növekedne a bevétel és ezzel a profit. Akármilyen is a megállapított ár és mennyiség, a két csoportban a határbevételnek azonosnak kell lennie.

Azt is tudjuk, hogy az összes kibocsátás akkor optimális, ha a határbevétel megegyezik a határköltséggel, mert ez biztosítja a maximális profitot. Ha a határbevétel egyezik is a két csoportban, de magasabb, mint a határköltség, akkor érdemes lesz növelni az értékesítést mindkét csoportban, mindaddig, míg a határbevétel és határköltség azonos nem lesz. A harmadfokú árdiszkrimináció esetén a profitmaximum második feltétele, hogy az egymással azonos határbevételeknek meg kell egyezniük a határköltséggel.

Ugyanerre az eredményre jutunk az algebrai levezetéssel is. Tegyük fel, hogy a monopólium két csoport, az A és a B piac között próbálja elosztani értékesítését, amelynek ismeri keresleti magatartását és el is tudja őket különíteni egymástól. (Például a diákbérletet csak a diákigazolvány felmutatásával lehet használni.)

Jelöljük Q_A-val A piacon értékesíteni kívánt mennyiséget, Q_B-vel a B piacra szánt termékmennyiséget, és Q-val e kettő összegét (azaz a monopólium által gyártott összes termék mennyiségét). Ekkor a vállalat profitfüggvénye:

(119)

A profitmaximum elsődleges feltétele szerint a határprofitnak nullának kell lennie.

(120)

(121)

Tudjuk azonban, hogy:

(122)

és

(123)

, és

(124)

ebből:

(125)

Ezzel a képlettel csupán az árarányokat tudjuk meghatározni, vagyis azt, hogy ha az A piacon a kereslet árrugalmassága nagyobb, akkor

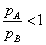(126)

Az egyes piacok árait a következőképpen határozhatjuk meg: Először a két részpiacra kapott határbevételi függvényt kell horizontálisan összegezni, hogy megkapjuk a összesített határbevételi függvényt. Ezt követően meg kell állapítani, hogy ez az összesített határbevételi függvény, mely Q értéknél metszi a határköltséget. Ez lesz az az optimális termelési mennyiség, amelyet később a részpiacok között kívánunk felosztani és egyben így kapjuk meg azt a határköltséget, amelyhez mindkét piac határbevételének igazodnia kell. Ebből meghatározhatjuk Q_A és Q_B értékét, illetve a hozzájuk tartozó árakat.

A harmadfokú árdiszkrimináció érvényesítésének fenti feltételei nem mindig teljesülnek, ezért hiába lehet elkülöníteni a fogyasztói csoportokat, a különböző ár megállapítása nem eredményezi a profit növelését. Nem érdemes például árdiszkriminációt alkalmazni akkor, ha az egyik csoport túl kicsi a másikhoz képest, vagy ha a keresleti függvények rugalmassága nem különbözik lényegesen egymástól.