| Vissza |
Mintafeladat
A Lerner-index számítása
Egy termék piacán a költségeket a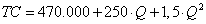 
összefüggés írja le.
Három esetet vizsgálunk, amelyekben a piac árérzékenysége különböző lesz. Az első két eset monopólium (különböző meredekségű keresleti függvényekkel), a harmadik eset a tökéletes verseny esete.
Az első esetben a keresleti függvény: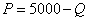 
A második eset keresleti függvénye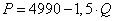 
A harmadik esethez tételezzük fel, hogy a piacon a tökéletes versenyző vállalatok összesített keresleti függvénye az a határköltség lesz, ami a monopolpiac esetében is érvényes. Keresleti függvényként az első eset keresleti függvényét használjuk.
Határozzuk meg a haszonkulcs nagyságát (vagyis a Lerner-indexet), valamint az árrugalmasságot az egyes esetekre!
1. eset
Használjuk az ismert MR=MC összefüggést az optimum meghatározásához!
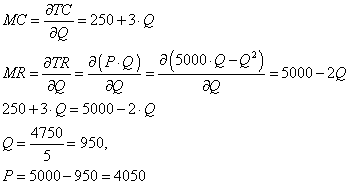
A 950 egységnyi termelési szinthez tartozó határköltség nagysága: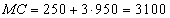 
A határbevétel (az optimumfeltétel miatt) szintén ezzel azonos értéket vesz fel, ugyanakkor nagysága meghatározható a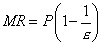 
képlet alapján is. A képletben a negatív előjel arra utal, hogy az árrugalmasság jellemzően negatív. Így ha a számításnál negatív értéket kapunk, akkor annak negativitása már a képletben szerepel, nem kell ezen felül is szerepeltetni!
Ha ezzel a módszerrel szeretnénk dolgozni, szükségünk van az optimumhoz tartozó árra, valamint az optimumban számított árrugalmasságra.
Az ár ismert, 950 egység.
Az árrugalmasság pedig az ismert képlet alapján (pontrugalmassági formulát alkalmazva):
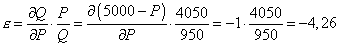
Így a határbevétel megkapható az előbb bemutatott módon, vagyis
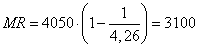, ami azonos eredményt ad mint a korábban látott megoldás.
A Lerner-index az ismert képlet alapján a következő értéket veszi fel:
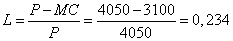, vagyis a haszonkulcs 23,4%-os.
A vállalati profit nagysága pedig a TR-TC összefüggésből
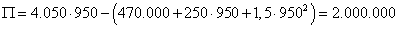
2. eset
Ha azonos költségek mellett a keresleti függvény meredekebbé válik (vagyis az árakra kevésbé érzékeny), akkor - az adott összefüggésekkel számolva a következő változások történnek:
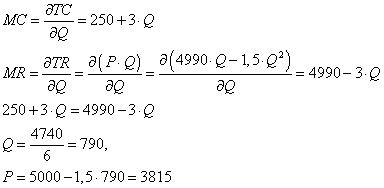
Az ehhez tartozó határköltség nagysága: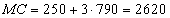 
Az árrugalmasság az optimumban:
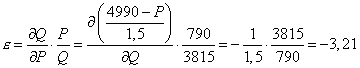
Amiből az határbevétel szintén 2620 egység kell, hogy legyen, vagyis
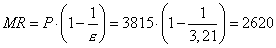. A két módszer tehát itt is azonos eredményre vezet.
A Lerner index nagysága ebben az esetben:
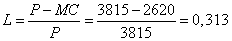, vagyis a haszonkulcs 31,3%-os.
A vállalati profit nagysága pedig a TR-TC összefüggésből
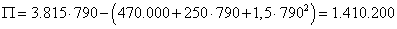
3. eset
A tökéletes verseny kínálati függvénye az egyéni (vállalati) határköltség-függvények összege. Feltevésünk szerint ez egyenlő az előző szerkezetekben látott határköltség-függvényekkel, vagyis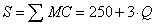 
A keresleti és a kínálati függvény metszéspontjában alakul ki az egyensúlyi ár, amely aztán a piac összes szereplője számára adottsággá válik:
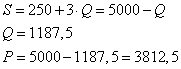
A tökéletes verseny esetében viszont az optimum feltétele az, hogy az MC=P összefüggés teljesüljön (hisz ebben a piaci szerkezetben a határbevétel és a piaci ár mindig egyenlő, így lesz az MC=MR összefüggésből MC=P).
Eszerint a határköltség szintén 3812,5 egység. Ezekből pedig a Lerner-index nagysága:
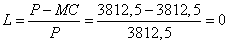, vagyis a haszonkulcs 0%-os.
Látszik tehát, hogy ahogy a keresleti függvény egyre rugalmasabbá válik, annál inkább csökken a haszonkulcs értéke. A három eset közül a legrugalmatlanabb kereslet a másodikban volt (hisz itt volt kisebb az árrugalmasság kiszámított értéke is), itt vette fel a Lerner-index a legmagasabb értéket. A leginkább rugalmas eset a tökéletes verseny volt (itt az árrugalmasság a használt képletekkel dolgozva végtelen lenne), a Lerner-index értéke ez esetben zérus.
| Vissza |